Definition

• A set is an unordered collection of distinct objects, called elements or members of the set.
• We write $a\in A$ to denote that a is an element of the $setA$.
• The notation $a\notin A$ denotes that a is not an element of the $setA$.

Representation

Enumerate

$$V=\{a,e,i,o,u\}$$

Set builder

$$O=\{x\mid \text{x is an odd positive integer less than 10}\}$$

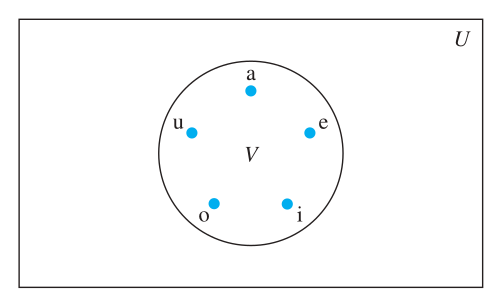
Venn Diagrams

Set Equality

• Two sets are equal if and only if they have the same elements.
• We write $A=B$ if A and B are equal sets.
• Therefore, if A and B are sets, then A and B are equal if and only if

$$A=B\leftrightarrow \mathrm{\forall }x(x\in A\leftrightarrow x\in B)$$

TIP

To show that two sets A and B are equal, show that $A\subseteq B$ and $B\subseteq A$

Empty set

• Empty set (null set): a special set that has no elements
• Notation: $S=\{\}\text{ OR }\mathrm{\varnothing }$
• Example: the set of all positive integers that are greater than their squares is the null set

Singleton set

• Singleton set: A set with one element is called a singleton set
• Example: $\{\mathrm{\varnothing }\}$ has one more element than $\mathrm{\varnothing }$

Subsets

• The set A is a subset of B, and B is a superset of A, if and only if every element of A is also an element of B.
• We use the notation $A\subseteq B$ to indicate that A is a subset of the set B.
• If, instead, we want to stress that B is a superset of A, we use the equivalent notation $B\supseteq A$
• We see that A ⊆ B if and only if the quantification:

$$\mathrm{\forall }x(x\in A\to x\in B)\text{ is true}$$

Proper subset

• That a set A is a subset of a set B but that $A\ne B$

$$A\subset B$$

• That is, A is a proper subset of B if and only if

$$\mathrm{\forall }x(x\in A\to x\in B)\wedge \mathrm{\exists }x(x\in B\wedge x\notin A)\text{ is true}$$

Theorem 1

$$\text{For every set S, }$$$$\text{ (i) }\mathrm{\varnothing }\subseteq S$$$$\text{(ii) }S\subseteq S$$

• Proof: We will prove (i )
  • Let S be a set.
  • To show that $\mathrm{\varnothing }\subseteq S$, we must show that:
    • $\forall x(x\in \mathrm{\varnothing }\to x\in S)$ is true.
  • Because the empty set contains no elements, it follows that $x\in \mathrm{\varnothing }$ is always false.
  • It follows that the conditional statement $x\in \mathrm{\varnothing }\to x\in S$ is always true, because its hypothes is always false and a conditional statement with a false hypothesis is true.
  • Note that this is an example of a vacuous proof.

The Size of a Set

• Let S be a set. If there are exactly n distinct elements in S where n is a non-negative integer,
• we say that S is a finite set and that n is the cardinality of S.
• The cardinality of S is denoted by

$$|S|$$

Power Sets

• Given a set S, the power set of S is the set of all subsets of the set S.
• The power set of S is denoted by

$$\mathcal{P}\{S\}$$$$|\mathcal{P}(S)|=2^{|S|}$$

• Example: The power set $P(\{0,1,2\})$ is the set of all subsets of $\{0,1,2\}$. Hence, $P(\{0,1,2\})=\{\varnothing ,\{0\},\{1\},\{2\},\{0,1\},\{0,2\},\{1,2\},\{0,1,2\}\}.$

Cartesian Products

Ordered n-tuples

• The ordered n-tuple $(a_1,a_2,\dots ,a_n)$ is the ordered collection that has $a_1$ as its first element, $a_2$ as its second element, … , and $a_n$ as its nth element.
• Let A and B be sets. The Cartesian product of A and B, denoted by $A\times B$, is the set of all ordered pairs (a, b), where a ∈ A and b ∈ B.
• Hence,

$$A\times B=\{(a,b)\mid a\in A\wedge b\in B\}$$

WARNING

Note that the Cartesian products A × B and B × A are not equal unless $A=\varnothing$ or $B=\varnothing$ or $A=B$

Generally for product of multiple sets

• We denote $A_1\times A_2\times \cdots \times A_n$ , is the set of ordered n-tuples $(a_1,a_2,\dots ,a_n)$, where $a_i$belongs to $A_i$ for i = 1, 2, … , n.
• In other words,

$$A1\times A2\times \cdots \times An=\{(a_1,a_2,\dots ,a_n)\mid a_i\in A_i\text{ for }i=1,2,\dots ,n\}$$

Using Set Notation with Quantifiers

• We restrict the domain of a quantified statement explicitly by making use of a particular notation

$$\forall x\in S(P(x))$$

• denotes the universal quantification of P(x) over all elements in the set S
• Ex: $\forall x\in R(x2\ge 0)$

Truth Sets and Quantifiers

• We will now tie together concepts from set theory and from predicate logic.
• Given a predicate P, and a domain D, we define the truth set of P to be the set of elements x in D for which P(x) is true.
• The truth set of P(x) is denoted by

$$\{x\in D\mid P(x)\}$$

• What are the truth sets of the predicates P(x) where the domain is the set of integers and P(x) is “|x| = 1,” . ⇒ The truth set of P, $\{x\in Z\mid |x|=1\}$, we see that the truth set of P is the set

• Note that $\forall xP(x)$ is true over the domain U if and only if the truth set of P is the set U.

• Likewise, $\exists xP(x)$ is true over the domain U if and only if the truth set of P is nonempty.