Sequences

• A sequence is a function from a subset of the set of integers (usually either the set $\{0,1,2,...\}$ or the set $\{1,2,3,...\}$) to a set S
• We use the notation $a_n$ to denote the image of the integer n
• We call $a_n$ a term of the sequence (term = phần tử)
• We use the notation $\{a_n\}$ to describe the sequence

Geometric progression (Cấp số nhân)

• A geometric progression is a sequence of the form

$$a,ar,a{r}^2,...,a{r}^n,...$$

• where the initial term $a$ and the common ratio $r$ are real numbers.
• In other words, A geometric progression is a discrete analogue of the exponential function

$$f(x)=a{r}^x$$

• Example:
  • The sequences $\{d_n\}$ with $d_n=6\cdot (1∕3{)}^n$
    • a = 6
    • r = 1/3

Arithmetic progression (Cấp số cộng)

• An arithmetic progression is a sequence of the form

$$a,a+d,a+2d,...,a+nd,...$$

• where the initial term $a$ and the common difference $d$ are real numbers.
• In other words, A arithmetic progression is a discrete analogue of the linear function

$$f(x)=dx+a$$

• Example:
  • The sequences $\{s_n\}$ with $s_n=-1+4n$
    • a = -1
    • d = 4

Recurrence Relations

• A recurrence relation for the sequence $\{an\}$ is an equation that expresses $a_n$ in terms of one or more of the previous terms of the sequence
• $a_0,a_1,...,a_n-1$, for all integers n with $n\ge n_0$, where $n_0$ is a nonnegative integer
• A sequence is called a solution of a recurrence relation if its terms satisfy the recurrence relation
• Example:
  • Let $\{a_n\}$ be a sequence that satisfies the recurrence relation $a_n=a_{n-1}-a_{n-2}$ for $n=2,3,4,...$ , and suppose that $a_0=3$ and $a_1=5$
  • ⇒ $a_2=2$, $a_3=-3$
• The $a_0\text{ and }{a}_1$ from the example is called initial conditions

Fibonacci sequence

• Initial conditions $f_0=0,f_1=1$
• Recurrence relation

$$f_n=f_{n-1}+f_{n-2}\text{ for }n=2,3,4,...$$

Closed formula

• We say that we have solved the recurrence relation together with the initial conditions when we find an explicit formula
• Example:
  • Let $\{a_n\}$ be a sequence that satisfies the recurrence relation $a_n=n{a}_{n-1}$ for $n=1,2,3,4,...$ , and suppose that $a_1=1$
  • ⇒ $a_n=n!$, the factorial function

Solve recurrence relations

Iteration

• Let $\{a_n\}$ be a sequence that satisfies the recurrence relation $a_n=a_{n-1}+3$ for $n=1,2,3,4,...$ , and suppose that $a_0=2$

Forward substitution

$$a_1=2+3$$$$a_2=(2+3)+3=2+3\cdot 2$$$$a_3=(2+2\cdot 3)+3=2+3\cdot 3$$$$a_n=2+3(n-1)$$

Backward substitution

$$a_n=a_{n-1}+3$$$$=(a_{n-2}+3)+3=a_{n-2}+3.2$$$$=(a_{n-3}+3)+3.2=a_{n-3}+3.3$$$$=2+3(n-1)$$

Special Integer Sequences

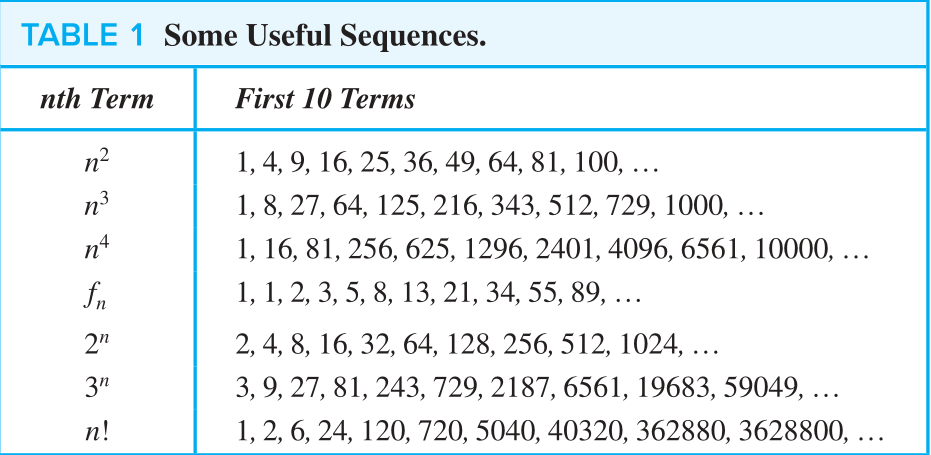
• Example:
  • How can we produce the terms of a sequence if the first 10 terms are $1,3,4,7,11,18,29,47,76,123$ ?
  • ⇒ $a_n=a_{n-1}+a_{n-2}$ with initial conditions are $a_0=1$, $a_1=3$