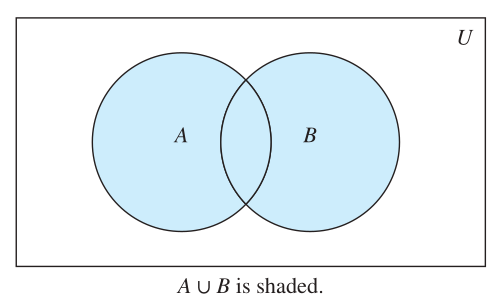
Union

• The union of the sets A and B, denoted by A ∪ B, is the set that contains those elements that are either in A or in B, or in both.

$$A\cup B=\{x\mid x\in A\vee x\in B\}.$$

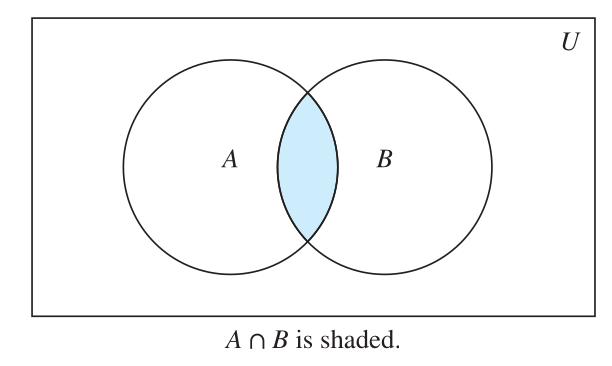
Intersection

• The intersection of the sets A and B, denoted by A ∩ B, is the set containing those elements in both A and B.

$$A\cap B=\{x\mid x\in A\wedge x\in B\}$$

Disjoint

Two sets are called disjoint if their intersection is the empty set.

$$A\cap B=\mathrm{\varnothing }$$

Principle of inclusion–exclusion

$$|A\cup B|=|A|+|B|-|A\cap B|$$

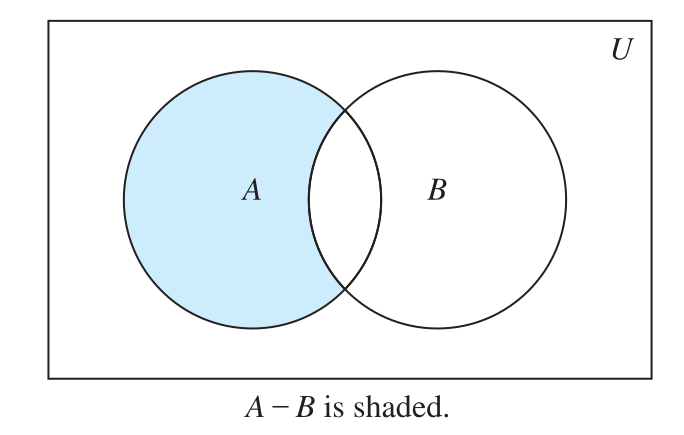
Difference

• The difference of A and B, denoted by A − B (A∖B), is the set containing those elements that are in A but not in B.
• The difference of A and B is also called the complement of B with respect to A.

$$A-B=A\setminus B=\{x\mid x\in A\wedge x\notin B\}$$

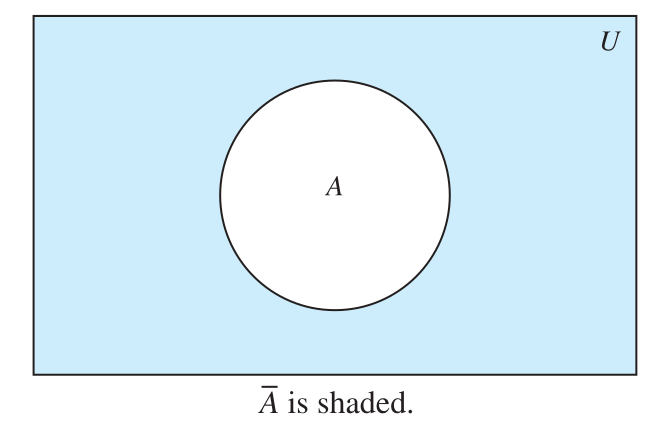
Complement

• Let U be the universal set. The complement of the set A, denoted by A, is the complement of A with respect to U.
• Therefore, the complement of the set A is U − A.

$$A=x\in U\mid x\notin A.$$

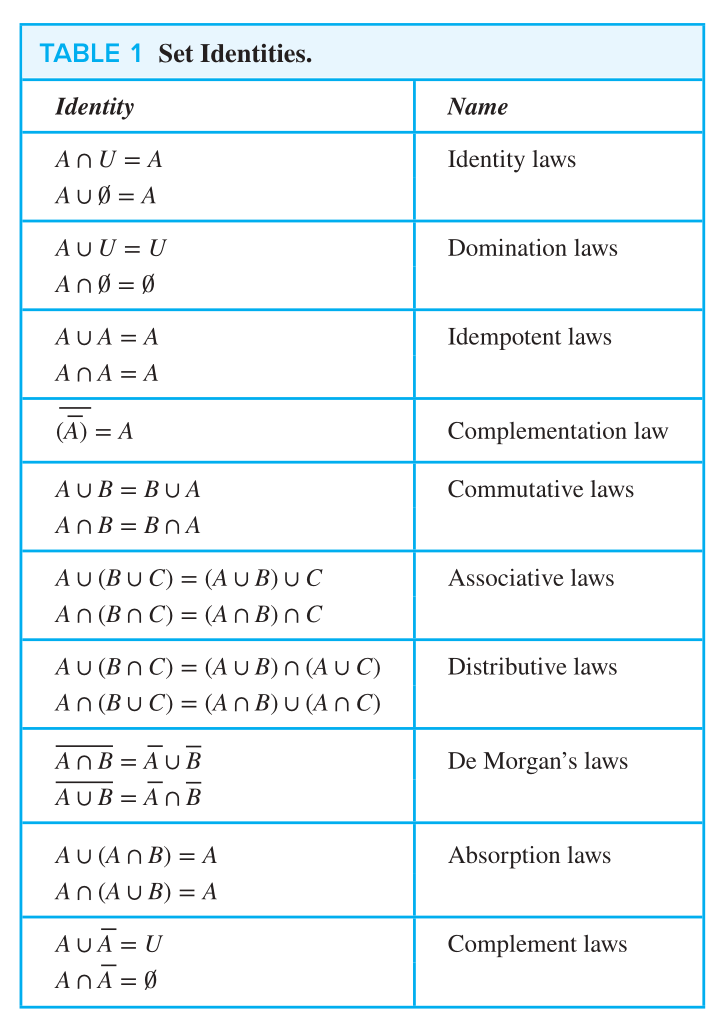
Set Identities

Methods of Proving Set Identities

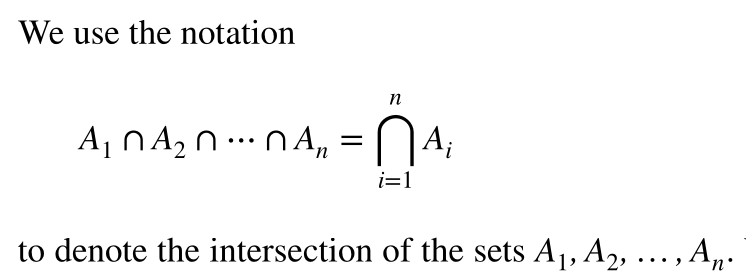
Generalized Unions and Intersections

• The union of a collection of sets is the set that contains those elements that are members of at least one set in the collection.

  

• The intersection of a collection of sets is the set that contains those elements that are members of all the sets in the collection.

  

Computer Representation of Sets

• Assume that the universal set U is finite
• First, specify an arbitrary ordering of the elements of U, for instance $a_1,a_2,...,a_n$ .
• Represent a subset A of U with the bit string of length n where the $i^{th}$ bit in this string is 1 if $a_i$ belongs to A and is 0 if $a_i$ does not belong to A
• Ex:
  • Let $U=\{1,2,3,4,5,6,7,8,9,10\}$ What bit strings represent the subset of all odd integers in U ?
  • A = $\{1,3,5,7,9\}$
  • Bit strings: $1010101010$

Multiset

• The number of times that an element occurs in an unordered collection matters.
• A multiset (short for a multiple-membership set) is an unordered collection of elements where an element can occur as a member more than once
• Ex: $A=\{a,a,a,b,b\}$ is the multiset that contains the element a thrice and the element b twice. Hence, $A=\{3.a,2.b\}$ where 3, 2 is called multiplicities

Union

• The union of the multisets P and Q is the multiset in which the multiplicity of an element is the maximum of its multiplicities in P and Q

Intersection

• The intersection of P and Q is the multiset in which the multiplicity of an element is the minimum of its multiplicities in P and Q.

Difference

• The difference of P and Q is the multiset in which the multiplicity of an element is the multiplicity of the element in P less its multiplicity in Q unless this difference is negative, in which case the multiplicity is 0

Sum

• The sum of P and Q is the multiset in which the multiplicity of an element is the sum of multiplicities in P and Q.