A red-black tree is a binary search tree with one extra bit of storage per node: its color

Properties

1

Every node is either RED or BLACK

2

The root is always BLACK

3

Every leaf (NIL) is BLACK

4

If a node is RED, then both its children are BLACK

=> Cannot have 2 consecutive nodes on a arbitrary simple path both are RED

5

For each node, all simple paths from the node to descendant leaves contain the same number of BLACK nodes.

Black-height

• We call the number of black nodes on any simple path from, but not including, a node x down to a leaf the black-height of the node, $bh(x)$
• The black-height of a red-black tree is the black-height of its root

Lemma

• A red-black tree with n internal nodes has height at most $2lg(n+1)$

Rotations

• Because they modify the tree, the result may violate the red-black properties
• The pointer structure changes through rotation, which is a local operation in a search tree that preserves the binary-search-tree property

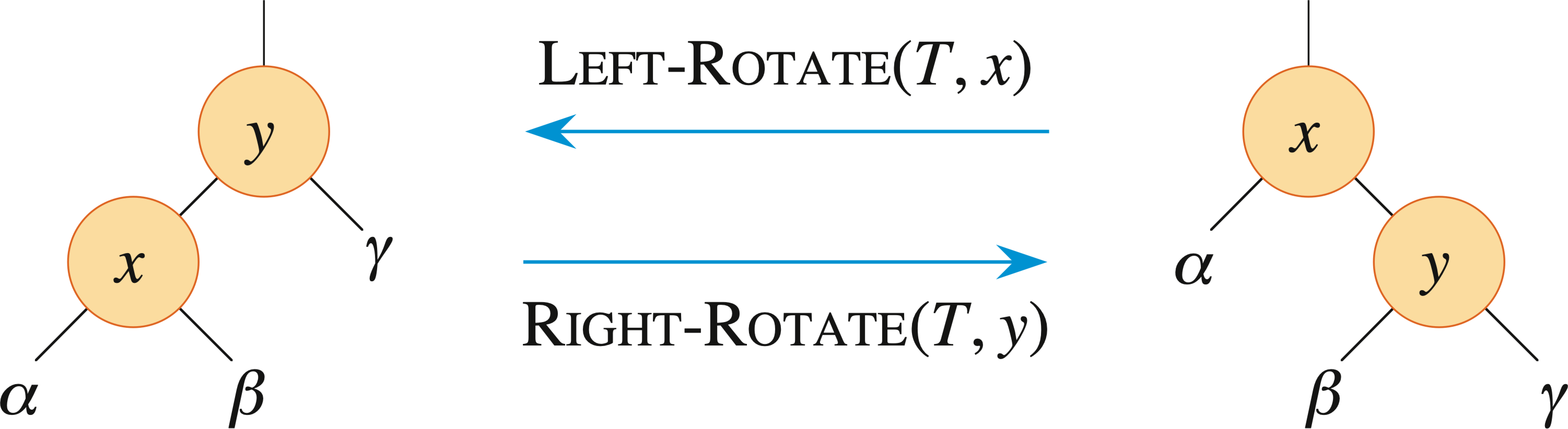
Insertion

• New node is always RED

What violations of the red-black properties might occur

• [x] 1. Every node is either RED or BLACK

  • Always true

• [ ] 2. The root is always BLACK

• [x] 3. Every leaf (NIL) is BLACK

  • Since both children of the newly inserted RED node are the NIL

• [ ] 4. If a node is RED, then both its children are BLACK

• [x] 5. For each node, all simple paths from the node to descendant leaves contain the same number of BLACK nodes.

  • Since new node is RED, then it does not violate the black-height

• We can see that 2 properties 2 and 4 can be violated

• Property 2 might be violated when newly RED node is root

• Property 4 might be violated when parent’s new RED node is also RED

💡

If the tree violates any of the red-black properties, then it violates at most one of them, and the violation is of either property 2 or property 4, but not both

• illustration