Primes

• An integer p greater than 1 is called prime if the only positive factors of p are 1 and p.
• A positive integer that is greater than 1 and is not prime is called composite, means if and only if there exists an integer a such that a ∣ n and 1 < a < n.

The fundamental theorem of arithmetic

🔑

Every integer greater than 1 can be written uniquely as a prime or as the product of two or more primes, where the prime factors are written in order of non-decreasing size.

Trial Division

Theorem 2

🔑

If n is a composite integer, then n has a prime divisor less than or equal to $\sqrt{n}$

• Proof:
  • From composite def, we have $n=a.b$ where b > 1
  • Proof that $a\le \sqrt{n}$ OR $b\le \sqrt{n}$
  • Assume, $a>\sqrt{n}$ AND $b>\sqrt{n}$, then $ab=\sqrt{n}\sqrt{n}=n>n$, contradict

💡

From Theorem 2, it follows that an integer is prime if it is not divisible by any prime less than or equal to its square root

Theorem 3

💡

There are infinitely many primes

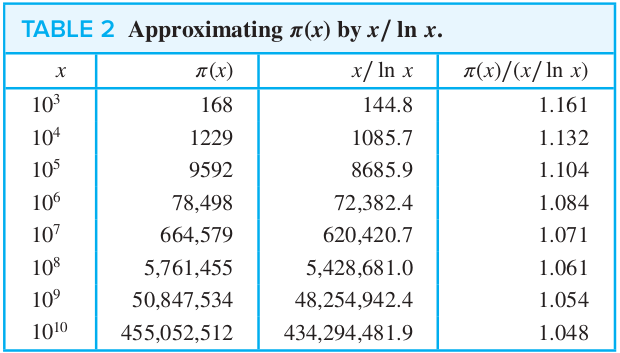
Theorem 4 (The prime number theorem)

💡

The ratio of $𝜋(x)$, the number of primes not exceeding x, and $x∕lnx$ approaches 1 as x grows without bound. (Here $lnx$ is the natural logarithm of x.)

Mean that,

💡

$$\underset{x\to \mathrm{\infty }}{lim}\frac{\pi (x)}{{\displaystyle \frac{x}{\log (x)}}}=1$$

Prime form

Greatest Common Divisors

• Let a and b be integers, not both zero. The largest integer d such that $d|a$ and $d\mid b$ is called the greatest common divisor of a and b. The greatest common divisor of a and b is denoted by $gcd(a,b)$

$$gcd(a,b)=1=>\text{a and b are relatively prime}$$

Algorithm

• To find the $gcd(a,b)$ is to use the prime factorizations of these integers
• Suppose we factorize a and b into,
  • $$\begin{gathered} a=p_1^{a_1}\cdot p_2^{a_2}\cdots \cdot p_n^{a_n} \\ b=p_1^{b_1}\cdot p_2^{b_2}\cdots \cdot p_n^{b_n} \end{gathered}$$
• Then,
  • $gcd(a,b)=p_1^{min(a_1,b_1)}\cdot p_2^{min(a_2,b_2)}\cdots \cdot p_n^{min(a_n,b_n)}$

Least Common Multiples

• The least common multiple of the positive integers a and b is the smallest positive integer that is divisible by both a and b. The least common multiple of a and b is denoted by $lcm(a,b).$

Algorithm

• Same as GCD but get $max(a_n,b_n)$
  • $lcm(a,b)=p_1^{max(a_1,b_1)}\cdot p_2^{max(a_2,b_2)}\cdots \cdot p_n^{max(a_n,b_n)}$

The relationship between GCD and LCM

💡

Let a and b be positive integers. Then $ab=gcd(a,b)\cdot lcm(a,b)$

The Euclidean Algorithm

💡

An efficiency algorithm to find $gcd(a,b)$

✅

Let $a=bq+r,$ where a, b, q, and r are integers. Then $gcd(a,b)=gcd(b,r)$

gcds as Linear Combinations

BÉZOUT’S THEOREM

• If a and b are positive integers, then there exist integers s and t such that,

$$gcd(a,b)=sa+tb$$

• This equation is called Bézout’s identity
• Two integers $s$ and $t$ are called Bézout coefficients of a and b

LEMMA 2

✅

If a, b, and c are positive integers such that gcd(a, b) = 1 and a ∣ bc, then a ∣ c.

LEMMA 3

✅

If p is a prime and p ∣ a1 a2 ⋯ an , where each ai is an integer, then p ∣ ai for some i.

THEOREM 7

✅

Let m be a positive integer and let a, b, and c be integers.

If $ac\equiv bc(modm)$ and $gcd(c,m)=1$,

⇒ $a\equiv b(modm)$.