Integer Representations

Theorem 1

• For any integer $b>1$ (the base) and any positive integer n, there is a unique representation:

$$n=a_k{b}^k+a_{k-1}{b}^{k-1}+\cdots +a_{1}b+a_0$$

where:

• $k\ge 0$ is an integer (the highest power of $b$ in the representation).
• $a_0,a_1,\dots ,a_k$ are digits, each satisfying $0\le a_i<b$.
• $a_k\ne 0$ (so the first digit is not zero, ensuring uniqueness).

💡

Theorem 1 is called the base b expansion of n

Expansions

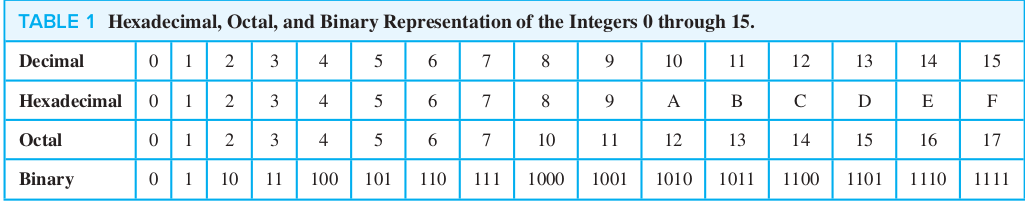
• Decimal: b = 10
• Binary : b = 2
• hexadecimal: b = 16
• Octal: b = 8

Base conversion

1. First, divide n by b to obtain a quotient and remainder, that is,

$$n=b{q}_0+a_0\text{ , where }0\le a_0<b$$

1. The remainder, $a_0$, is the rightmost digit in the base b expansion of n. Next, divide $q_0$ by b to obtain

$$q_0=b{q}_1+a_1\text{ , where }0\le a_1<b$$

1. $a_1$ is the second digit from the right in the base b expansion of n
2. Continue this process until we obtain a quotient equal to zero.

Algorithm

Conversion between 2, 16 and 8 expansions

• Each octal digit corresponds to a block of three binary digits
• Each hexadecimal digit corresponds to a block of four binary digits

Algorithms for Integer Operations

✅

The algorithms for performing operations with integers using their binary expansions are extremely important in computer arithmetic

Throughout this discussion, suppose that the binary expansions of a and b are

$$\begin{gathered} a=(a_{n-1}{a}_{n-2}...a_1{a}_0{)}_2, \\ b=(b_{n-1}{b}_{n-2}...b_1{b}_0{)}_2 \end{gathered}$$

so that a and b each have n bits

Addition algorithm

1. To add a and b, first add their rightmost bits. This gives

$$a_0+b_0=c_0\cdot 2+s_0$$

• where
  • $s_0$ is the rightmost bit (LSB) in the binary expansion of a + b
  • $c_0$ is the carry, which is either 0 or 1

1. Then add the next pair of bits and the carry,

$$a_1+b_1+c_0=c_1\cdot 2+s_1$$

• where
  • $s_1$ is the next bit (from the right) in the binary expansion of a + b
  • $c_1$ is carry

1. Continue this process
2. At the last stage,

$$a_{n-1}+b_{n-1}+c_{n-2}=c_{n-1}\cdot 2+s_{n-1}$$

• Then, the leading bit of the sum is $s_n=c_{n-1}$

✅

$a+b=(s_n{s}_{n-1}{s}_{n-2}...s_1{s}_0{)}_2$

Multiplication algorithm

• Using the distributive law, we see that

$$ab=a(b_0{2}^0+b_1{2}^1+\cdots +b_{n-1}{2}^{n-1})=a(b_0{2}^0)+a(b_1{2}^1)+\cdots +a(b_{n-1}{2}^{n-1})$$

• We first note that:

1. • $a{b}_j=a$ if $b_j=1$
   • $a{b}_j=0$ if $b_j=0$
2. Each time we multiply a term by 2, we shift its binary expansion one place to the left and add a zero at the tail end of the expansion:

$$a\cdot 2^1=a<<1$$$$a\cdot 2^n=a<<n$$

3. Consequently, we can get $(a{b}_j)2^j$ by shifting the binary expansion of abj j places to the left, that

$$(a{b}_j)2^j=(a{b}_j)<<j$$

4. Finally, we get $ab$ by adding the n integers $a{b}_j{2}^j$, j = 0, 1, 2, ... , n − 1.

• Pseudocode

Algorithm for DIV and MOD

• This algorithm takes $O(qloga)$ bit operations

Modular Exponentiation

• How to find efficiently without using an excessive amount of memory for

$$b^{n}modm\text{ -- where b, n and m are large integers}$$

• Some thought,
  1. It is impractical to first compute $b^n$ and then find its remainder when divided by m, because $b^n$ can be a huge number
  2. We can apply Corollary 2 of Theorem 5 at [4.1] Divisibility and Modular which is

$$(ab)modm=((amodm)(bmodm))modm$$

Then, we have (Recall that $1\le b<m$)

$$b^{k+1}modm=b(b^{k}modm)modm$$

However, this approach is impractical because it requires n − 1 multiplications of integers and n might be huge.

Fast modular exponentiation algorithm

• Note that, If we use the base 2 expansion of n, then

$$\begin{gathered} b^n=b^{a_{k-1}\cdot 2^{k-1}+...a_1\cdot 2+a_0} \\ =b^{a_{k-1}\cdot 2^{k-1}}\cdot ...\cdot b^{a_1\cdot 2}\cdot b^{a_0} \end{gathered}$$

• This shows that to compute $b^n$, we need only compute the values of
  • $b,b^2,(b^2{)}^2=b^4,(b^4{)}^2=b^8,...,(b^{2^n}{)}^2=b^{2^k}$
• The algorithm successively finds
  • $bmodm$,
  • $b^{2}modm$,
  • $b^{4}modm$, ... ,
  • $b^{2^{k-1}}modm$ and
  • multiplies together those terms $b^{2^j}modm$ where $a_j=1$

Cantor Expansion

Definition

A Cantor expansion represents a non-negative integer as

$$n=a_{k}k!+a_{k-1}(k-1)!+\cdots +a_{2}2!+a_{1}1!$$

where

$$0\le a_i\le i\text{for }i=1,2,\dots ,k$$

This representation is also known as the factorial number system.

---

Properties

1. Uniqueness

Every non-negative integer has a unique Cantor expansion.

2. Mixed radix system

Cantor expansion is not a fixed-base system. The radix at position $i$ is $(i+1)$.

3. Bounded digits

Each coefficient has a strict bound:

• $a_1\in \{0,1\}$
• $a_2\in \{0,1,2\}$
• $\dots$
• $a_k\in \{0,1,\dots ,k\}$

---

Finding the Cantor Expansion

Algorithm

Given an integer $N$:

1. Find the largest $k$ such that $k!\le N$
2. Compute$$a_k=\lfloor \frac{N}{k!}\rfloor$$
3. Update$$N\leftarrow N-a_{k}k!$$
4. Repeat for $(k-1)!,(k-2)!,\dots ,1!$

---

Example

Find the Cantor expansion of $1000$.

$$(1,2,1,2,2,0)$$

---

Why Cantor Expansion Works

Because

$$1!+2!+\cdots +k!<(k+1)!$$

this guarantees:

• No overlap between representations
• Each sequence $(a_1,\dots ,a_k)$ maps to a distinct integer