TIP

Functions are sometimes also called mappings or transformations.

Function, domain, codomain, range

• Let A and B be nonempty sets.
• A function $f$ from A to B is an assignment of exactly one element of B to each element of A. We write $f(a)=b$ if $b$ is the unique element of B assigned by the function $f$ to the element $a$ of A.
• If $f$ is a function from A to B, we write

$$f:A\to B$$

• Where,

  • $A$ is the domain of $f$ (Tập xác định, TXĐ)
  • $B$ is the codomain of $f$ (Tập giá trị / Tập đích)

• If $f(a)=b$, we say that b is the image of a and a is a preimage of b. (ảnh và nghịch ảnh)

• if f is a function from A to B, we say that f maps A to B. (ánh xạ)

• A function $f:A\to B$ can also be defined in terms of a relation from A to B (just a subset of 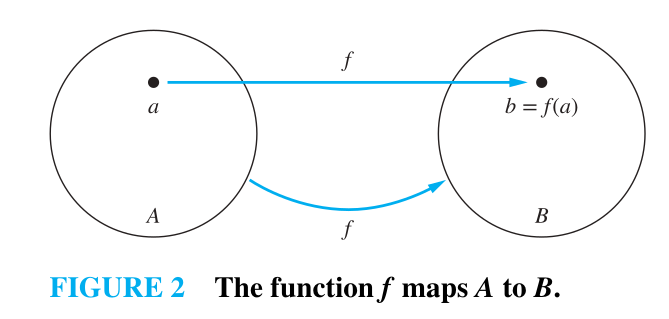$A\times B$)

  

• The range is the set of all values of $f(a)\text{ for }a\in A$, and is always a subset of the codomain. In other words, range is actually created set.

• Example,

  • Let $f:Z\to Z$, $f(x)=x^2$,
    • Domain of f is all integers
    • Codomain of f is all integers
    • Range of f is $\{0,1,2,4,9,\dots \}$

Function equality

• Two functions are equal when they have
  • The same domain
  • The same codomain
  • Map each element of their common domain to the same element in their common codomain (tức là $f(a)=g(a)$ với mọi a)

Sum and product

• Let $f_1$ and $f_2$ be functions from $A\text{ to }R$.
• Then $f_1+f_2$ and $f_1$ $f_2$ are also functions from $A$ to $R$ defined $\mathrm{\forall }x\in A$ by

$$(f_1+f_2)(x)=f_1(x)+f_2(x)$$$$(f_1{f}_2)(x)=f_1(x)f_2(x)$$

Set of images

Let $S$ be a subset of $A$, The image of $S$ under the function $f$ is the subset of $B$ that consists of the images of the elements of $S$

$$f(S)=\{t\mid \mathrm{\exists }s\in S(t=f(s))\}$$

Or, for shorthand

$$\{f(s)\mid s\in S\}$$

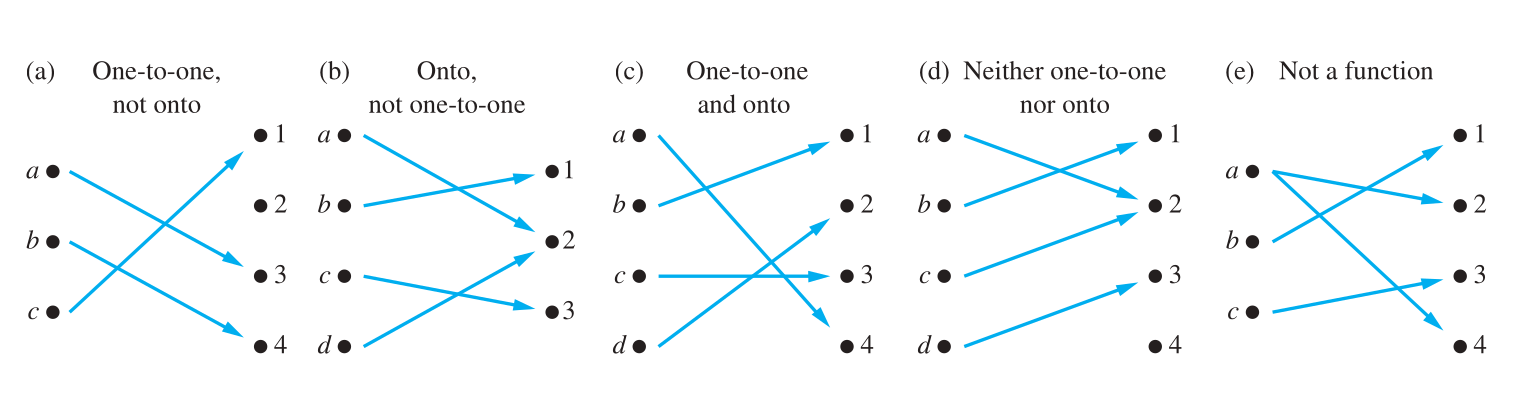
One-to-One and Onto Functions

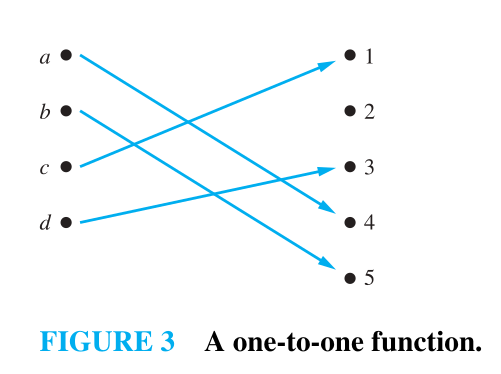
One-to-one (injective) function

• A function $f$ is said to be one-to-one, or an injection, if and only if $f(a)=f(b)$ implies that $a=b$ for all a and b in the domain of $f$.
• A function is said to be injective if it is one-to-one.
• In other words,
  • Note that a function f is one-to-one if and only if $f(a)\ne f(b)$ whenever $a\ne b$
• We can express that f is one-to-one using quantifiers

$$\mathrm{\forall }a\mathrm{\forall }b(f(a)=f(b)\to a=b)$$

Or using contrapositive,

$$\mathrm{\forall }a\mathrm{\forall }b(a\ne b\to f(a)\ne f(b))$$

• Example:
  • The function $f(x)=x^2$ with domain $Z^{+}$ is one-to-one
  • $f(x)=x+1$ with domain $R$ is one-to-one

Increasing/decreasing functions

• Hàm đồng biến/ nghịch biến
• A function $f$ whose domain and codomain are subsets of the set of real numbers is called increasing if $f(x)\le f(y)$, and strictly increasing if $f(x)<f(y)$, whenever $x<y$ and x and y are in the domain of f. Hence

$$\text{Increasing: }\mathrm{\forall }x\mathrm{\forall }y(x<y\to f(x)\le f(y))$$$$\text{Strictly Increasing: }\mathrm{\forall }x\mathrm{\forall }y(x<y\to f(x)<f(y))$$

• Similarly, for decreasing functions

$$\text{Decreasing: }\mathrm{\forall }x\mathrm{\forall }y(x<y\to f(x)\ge f(y))$$$$\text{Strictly Decreasing: }\mathrm{\forall }x\mathrm{\forall }y(x<y\to f(x)>f(y))$$

TIP

If a function either strictly increasing or strictly decreasing ⇒ that function is one-to-one

If a function either increasing or decreasing ⇒ that function is not one-to-one

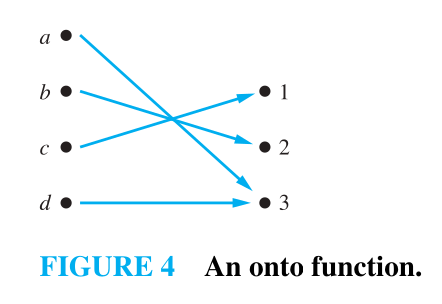
Onto (surjective) function (Hàm toàn)

• For some functions the range and the codomain are equal
• A function f from A to B is called onto, or a surjection, if and only if for every element $b\in B$ there is an element $a\in A$ with $f(a)=b$.
• A function f is called surjective if it is onto.

$$\mathrm{\forall }y\mathrm{\exists }x(f(x)=y)$$

Bijective function (Hàm song ánh)

• The function f is a one-to-one correspondence, or a bijection, if it is both one-to-one and onto.
• We also say that such a function is bijective.

Function Key Takeaway

Inverse Functions and Compositions of Functions

Inverse function

• Let f be a one-to-one correspondence from the set A to the set B.
• The inverse function of f is the function that assigns to an element b belonging to B the unique element a in A such that f (a) = b.
• The inverse function of f is denoted by $f^{-1}$ . Hence, $f^{-1}(b)=a$ when $f(a)=b$

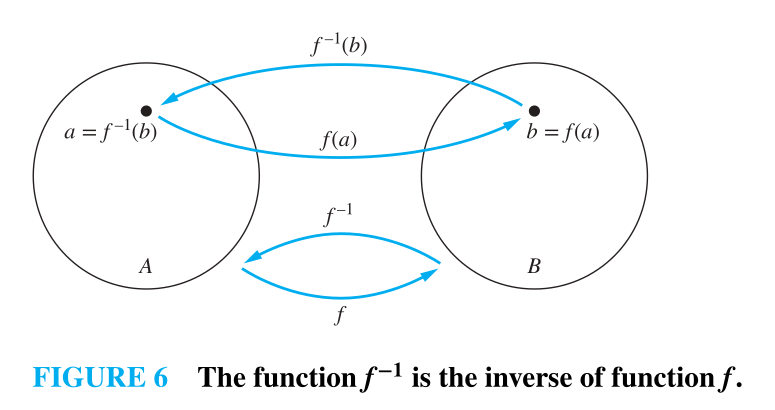
TIP

A one-to-one correspondence is called invertible because we can define an inverse of this function.

A function is not invertible if it is not a one-to-one correspondence, because the inverse of such a function does not exist.

Composition functions

• Let $g$ be a function from the set A to the set B and let $f$ be a function from the set B to the set C. The composition of the functions f and g, denoted for all $a\in A$ by $f\circ g$, is the function from A to C defined by

$$(f\circ g)(a)=f(g(a))$$

• Domain of $f\circ g$ is domain of $g$
• Range of $f\circ g$ is image of the range of $g$ with respect to the function $f$
• To find $(f\circ g)(a)$ we first apply the function g to a to obtain $g(a)$ and then we apply the function f to the result $g(a)$ to obtain $f(g(a))$

TIP

The composition $f\circ g$ cannot be defined if the range of g is not a subset of the domain of f. In other words, to be defined composition, this property must satisfy

$range(g)\subseteq domain(f)$

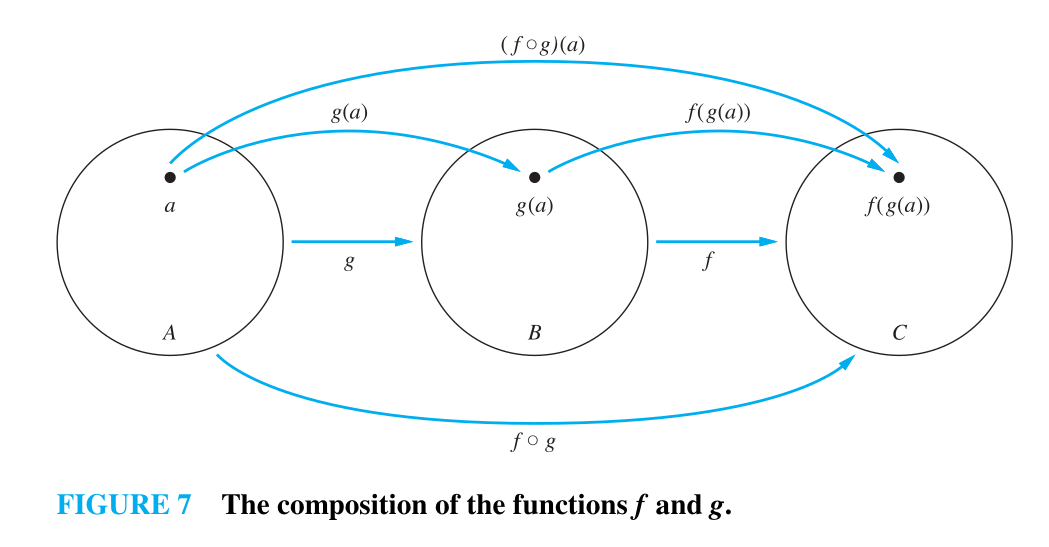
TIP

$f\circ g$ and $g\circ f$ are not equal

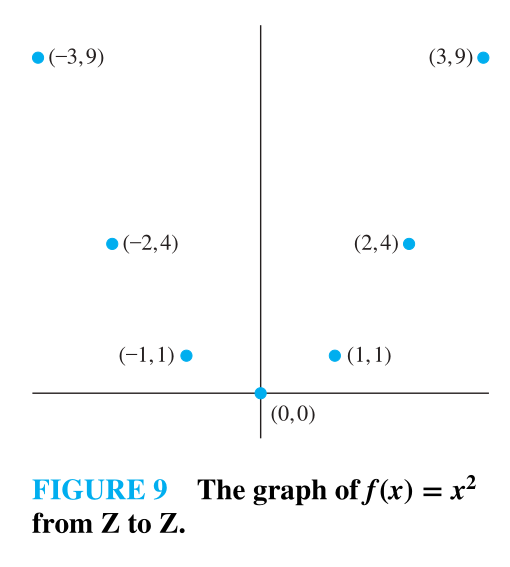
The Graphs of Functions (Đồ thị)

• Let f be a function from the set A to the set B. The graph of the function f is the set of ordered pairs

$$\{(a,b)\mid a\in A\text{ and }f(a)=b\}$$

Some Important Functions

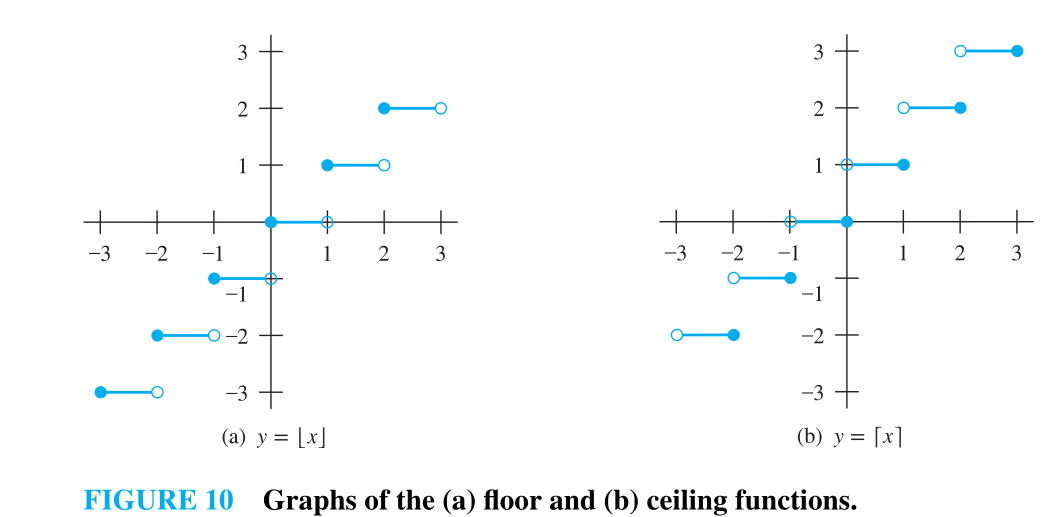
Floor function

• The floor function assigns to the real number x the largest integer that is less than or equal to x. The value of the floor function at x is denoted by

$$\lfloor x\rfloor$$

Ceiling function

• The ceiling function assigns to the real number x the smallest integer that is greater than or equal to x. The value of the ceiling function at x is denoted by

$$\lceil x\rceil$$

Useful properties of floor and ceiling functions

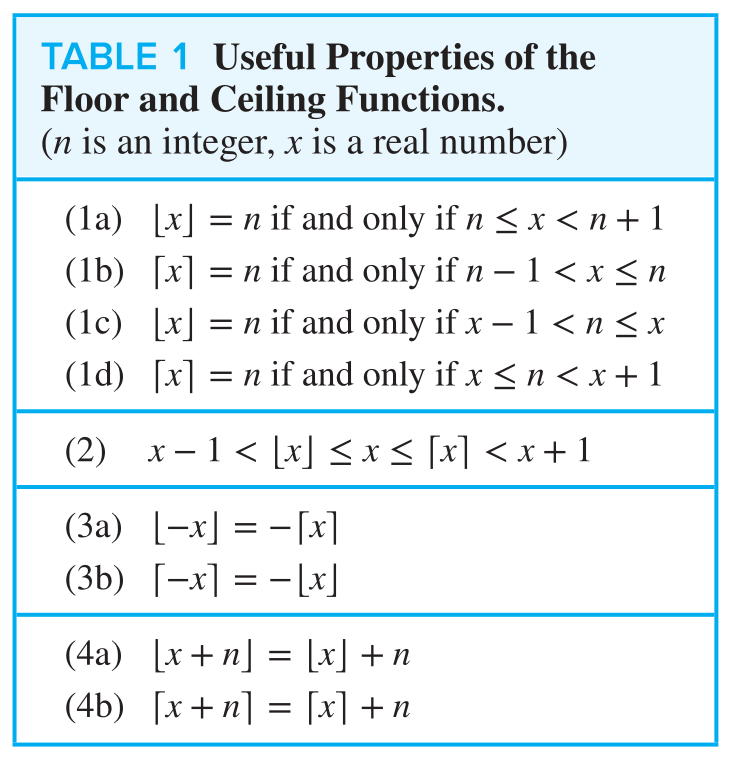
• A useful approach for considering statements about the floor function is to let $x=n+\epsilon$ , where $n=\lfloor x\rfloor$ is an integer, and $\epsilon$, the fractional part of x, satisfies the inequality $0\le \epsilon <1$
• Similarly, when considering statements about the ceiling function, we have

$$x=n-\epsilon \text{ with }0\le \epsilon <1$$

Partition functions (hàm từng phần)

• Chỉ định nghĩa trên một phần của tập A (không phải tất cả)
• Example:
  • $f:Z\to Z,f(x)=\frac{1}{x}$
  • undefined at x = 0, ⇒ partial function

Total functions (hàm toàn phần)

• Được định nghĩa cho mọi phần tử trong A. Không bỏ sót phần tử nào.